I’m learning game theory these days, and I’ve tried my hand at some problems inspired by ML theory. Here’s one I found really interesting.
Let’s assume the following (clearly unrealistic) situation:
- Working class (A) and bourgeoisie (B) form perfectly cooperative coalitions.
- They may negotiate salaries, with no class having any mechanism to obtain a better bargaining position.
- A cooperatively owns some amount k of capital, while B owns (arbitrarily) 1. In principle, k < 1.
- B has some labor power b, while A has (arbitrarily) 1. Again, b < 1.
- Production follows a Cobb-Douglas function, where the sum of the output elasticities of capital and labor is 1.
- Both classes consume the same proportion of their income and use the remainder to acquire more capital.
Therefore, the payoffs in our problem can be stated like this (where w is the labor given to B and s is the compensation given to A for this labor):
X_A = A k**α (1 - w)**β + s
X_B = A (b + w)**β - s
We would like to find how the ratio of A’s capital to B’s changes over time, so we compute its derivative using the quotient rule, and note that the proportion of income (p) spent on capital is the same for both classes:
R = p X_A - k p X_B
Finally, we find the Nash equilibrium and its corresponding R at each combination of k and b:
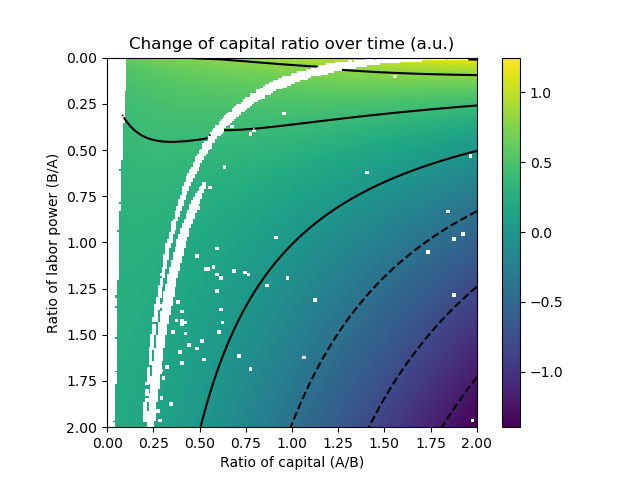
Note the attractor curve coinciding with k = 1/b. In other words, if both k and b are higher than 0, the eventual equilibrium will be for A and B to own capital proportional to their labor power.
Edit: fixed some missing solutions near k = 0.

Interesting, that’s a great conclusion to extract.
I would like to see next how much difference in expenses can be tolerated. Since the model predicts a higher R in the salary region than I expected, that seems to indicate at least some headroom for disadvantage, which might increase with improvements in productivity and decrease with attempts by the bourgoise class to make negotiation asymmetrical.
I wonder if analyzing the more general case could show the relationship between the development of productive forces and the various mechanisms of capitalism.
Anything else I should note? This is turning out to be an even more interesting learning path than I thought :)
Depreciation. It’s something a lot of people don’t think about, but from a Marxist standpoint, the depreciation of capital goods is actually quite central to the ubderstanding of capitalism.
Depreciation actually caps the total amount of capital that a population can accumulate, as beyond a certain point, all of the populations labor power will have to be spend replacing damaged capital goods.
This is actually the reason why the rate of profit falls in advanced economies (high capital -> high maintainance costs).
I am curious to see how adding Depreciation to your model will change things.
Always nice to see people explore the materialist side of Marxism.
Noted, thanks a lot!