I’m learning game theory these days, and I’ve tried my hand at some problems inspired by ML theory. Here’s one I found really interesting.
Let’s assume the following (clearly unrealistic) situation:
- Working class (A) and bourgeoisie (B) form perfectly cooperative coalitions.
- They may negotiate salaries, with no class having any mechanism to obtain a better bargaining position.
- A cooperatively owns some amount k of capital, while B owns (arbitrarily) 1. In principle, k < 1.
- B has some labor power b, while A has (arbitrarily) 1. Again, b < 1.
- Production follows a Cobb-Douglas function, where the sum of the output elasticities of capital and labor is 1.
- Both classes consume the same proportion of their income and use the remainder to acquire more capital.
Therefore, the payoffs in our problem can be stated like this (where w is the labor given to B and s is the compensation given to A for this labor):
X_A = A k**α (1 - w)**β + s
X_B = A (b + w)**β - s
We would like to find how the ratio of A’s capital to B’s changes over time, so we compute its derivative using the quotient rule, and note that the proportion of income (p) spent on capital is the same for both classes:
R = p X_A - k p X_B
Finally, we find the Nash equilibrium and its corresponding R at each combination of k and b:
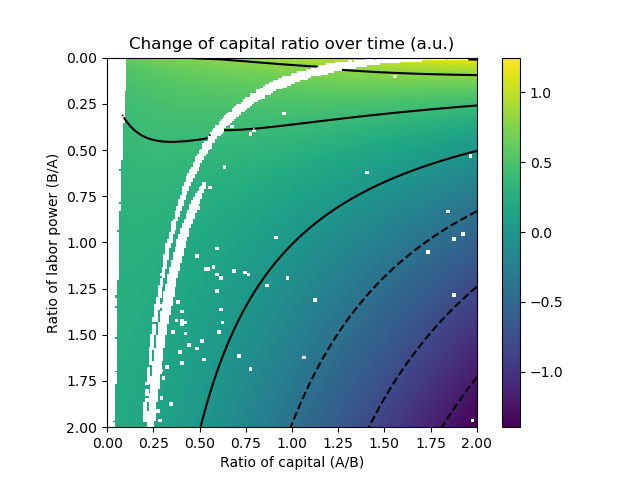
Note the attractor curve coinciding with k = 1/b. In other words, if both k and b are higher than 0, the eventual equilibrium will be for A and B to own capital proportional to their labor power.
Edit: fixed some missing solutions near k = 0.


If I understand correctly the graph, there are 3 distinct regions.
The very small region at the to where R>1, that seems to imply a situation where A and B would sort of switch roles, A would own most of the capital and B would own little to no capital and would live off of their labor power.
The large middle “north-east” region where 1>R>0, where B’s capital increases faster than A’s. Itself made up of 3 regions, one where A does most of the labor and own little to no capital, one where A does little work despite owning little to no capital, and one where A work little and own most capital similar to the first big region.
And the bottom right corner region where R<0, where either A or B is losing capital, but I’m not sure which.
Not exactly. The region where A and B would switch roles is near the bottom right, that’s why R is negative (both gain capital, but B gains it faster).
Beyond the first solid line, A and B both live off their own capital, but A has more manpower to capital ratio, and therefore makes better use of its capital.
Beyond the white line, A works for B (the expected initial state). Instead of increasing B’s capital faster than A’s, this model suggests A would be able to bargain a salary that, while benefiting both, would let A grow even faster than expected from capital and labor alone.
I don’t think I understand how the model works.
What is R exactly and how do you get it from X_A and X_B. And what are X_A and X_B in the first place?
The Xs are the total profits obtained by the two classes. R is the derivative of the ratio of capital with respect to time, k_A/k_B, where the derivative of each is assumed to be proportional to its corresponding X (the constant being p), and k_A = k while k_B = 1.
Why is it R = p X_A - k p X_B? Shouldn’t it be R = (p X_A) / (k p X_B)?
It’s the quotient rule for derivatives.