So I found out about Marx’ mathematical manuscripts, so I say “Hey, I’ve been studying mathematics this year at university. I understand limits and derivatives, maybe I can understand something of that gibberish.” So I see the titles and the one called “On the Concept of the Derived Function”, I go there and I see some notation I don’t understand, he speaks about things I’m not clearly understanding, so maybe some of you could make it clear.
For example:
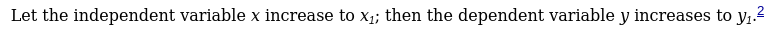
Why is this x sub 1 notation? Is this some other way to write derivatives? Because on the footnotes it says this:
- In order to avoid confusion with the designation of derivatives, Marx’s notation x´, y´, … for the new values of the variable has been replaced here and in all similar cases by x1, y1, …
Then I saw a talk about Marx’s mathematics and the infinitesimal and some of that stuff, but the one who was speaking didn’t went much into the mathematical part but was more like a history talk on how the Chinese were interested in the propositions of Marx because it liberated calculus from the idealist veil with which it was conceived by Leibniz and Newton, but the one who was talking mentioned Marx learning mathematics with whatever he had around and didn’t managed to read Cauchy so we was like “Yeah this is nice but it’s al shit now we have proved it fully works.” But well, he seems a bit biased, since he’s a Usonian, so maybe Marx’s writings are still relevant, I don’t even know who the fuck Cauchy is, so yeah, help.
Text: https://www.marxists.org/archive/marx/works/1881/mathematical-manuscripts/ch03.html


Yeah, I was taught these ideas using different letters for the variables and since I mentioned I am a beginner, I am in my first year of computer engineering so it still takes me some time until I see a formula and get to understand what it’s doing. Basically they taught me what functions are, intervals, inequations, movement of functions in a graph by modifying their variables, limits, derivatives, and function analysis, the subject was called “Introduction to Mathematical Analysis”, so we saw algebra, calculus, but not as individual subjects so yeah, I still need more practice but I think I get the idea here.
Ahhh, so the dx and dy basically represent that. Yes, we saw this, this is what happens when you divide by a number infinitely closer to 0 which, if it is positive, results in a positive infinite, and if it is negative gives you a negative infinite. So basically dx could be something that produces a value like 00000000000000000000000.1 for example? Of course this could keep getting closer to 0 till infinity. And yeah, this is basically the same method to apply in physics to calculate the average velocity of a particle, only there you usually work with more tangible spaces (meters, centimeters, instead of abstract ideas of infinite), but it basically comes down to calculating the difference in change from one point to the other from both axis.
So this theory proposed by L/N was considered flawed because dx/dy is not actually a numerical value but rather an idea, which can’t be hard proofed. That’s why Engels says this:
Because basically the theories proposed by them wasn’t hard proofed because you were not dealing with numbers but with abstract ideas.
I understand that Archimedes kind of got the idea of the infinite series, do you mean that?
Well, my main doubt was how much of this texts by Marx still hold up, because from Dauben’s talk it makes it seem as if after Cauchy’s they would have become obsolete and if Marx’s work on calculus and Cauchy’s works contradict each other or if they are compatible. Moreover, would these manuscripts an attempt by Marx to formalize the infinitesimal previously or contemporaneously to Cauchy? Because I think Cauchy’s works were available while Marx was alive but he didn’t managed to read them. And one more question, is there some relation between all this and the idea by Newton that space and time are unrelated as stated in the picture below?
I am truly seriously graceful for your help and your time, you helped me out and while my understanding of these topics is still bland and imperfect I feel I get a better grasp than before. Welcome to Lemmygrad, by the way, hope you are liking it so far!
As promised a few links to consider as well:
As a bit of an organizational note, I will be making the primary effort to answer your primary question, and then afterwards I’ll be jumping around to other parts of your post to answer some of the questions that I saw or reflect on some other miscellaneous things.
So to begin I think here is the best place to start:
So there are a couple questions baked in here but I believe the best way to begin is to just go straight to the conclusion and say that: Marx’s Manuscripts do still hold up because they do indeed capture the fundamental ideas of calculus in a much easier to understand way than the formal axiomatic approach, and a skilled mathematician with enough of an understanding of dialectical materialism could use these manuscripts as a starting off point to attack all of the sorts of “institutionalized” aspects of mathematics as it is done around the world. I’ll say that the western institution of mathematics adopts a philosophy that is grotesquely Liberal, and it’s not easy to see why because there really isn’t a lot of work on Marx and Engels and their commentary on mathematics. I will provide a few extra links at the bottom, if your interested in more on this.
Dauben doesn’t really say that Cauchy and Marx would’ve contradicted each other, it has been a bit of time since I’ve listened to that lecture but the best way I would describe it, would be to say that Cauchy represents the idealist desire of mathematicians (and mathematics as whole) to pull their abstractions out of a box and never return them to the real world. They do not know where the abstractions come from nor do they even know how they got into the box! This is a greater problem with mathematics. But that does not mean that “mathematics” is fake in a sense for example here writes Engels:
Here we see the same attack that any Marxist mathematician should be making against mathematics, and indeed, it is Marx that in a sense does develop some ideas of Calculus which are indeed also proven by formal methods, but without ever using formalism… To sum up what I’m trying to say: the Mathematical Manuscripts hold in them a very distilled example of the methodology of dialectical materialism towards the sciences and mathematics. It’s like having a flake of gold that proves that there is some gold in the hill. Also this manuscript should be used by non-mathematicians to study the exact nature of the methodology that Marx and Engels proposes because it clearly shows how Marx uses the concept of an infinitesimal to inquire about it dialectically and then go on to develop more concepts and so on. It is basically a robust exercise in applying dialectical materialism.
Onto the rest of the post:
I wouldn’t say that Marx appears to be trying to formalize anything, really I think the best characterization would be the one I put forward which is that it really is a very clear window into the mind of Marx on using dialectics to develop ideas in mathematics from very basic observations about the so-called “real” behavior of numbers.
Well certainly the theory of general relativity that Einstein puts forward does indeed link space and time, and ironically it may have been the most famous contemporary example of the relationship between mathematics and physics, because an area of mathematics called differential geometry was in fact developed ahead of Einsteins work on relativity, which in fact essentially inspired the whole theory. And we indeed do build the differential based on this more “formalized” version in modern mathematics, but I should stress that there is no reason why this same process could not be undertaken to explore differential geometry dialectically. Perhaps even it could be of major benefit towards the synthesis of the two competing theories in physics between relativity and quantum field theory. I believe as well that the part where Mao quotes Lenin is again another example of the dialectical process of development in mathematics and science, where we conceptualize in terms of mathematics and we observe in terms of real measurements, and the mathematics helps to develop our observations, and the observations in turn develop our math, with each getting closer and closer to each other, but ultimately because of how conceptions are just shadows of our interpretation of reality, and so our understanding of each is shaped dialectically but not in the sense of the two coming into one, but in the sense that the one (the thing we would like to know) drives this contradiction between the conceptualizations we make for describing reality in mathematics, and the actual observations of reality in science, and that that contradiction drives each of them forward.
So basically
+dxor-dxshould be thought of just a value like 0.00000000…001. It doesn’t really produce any sort of value, it is just a notational piece to denote “an infinitesimal positive or negative nudge in x”. In fact as you continue on there will be lots of these little mathematical notational things that are just there because in some sense they represent mathematical ideas instead of numerical things, and they are more like “the language of mathematics”. Which is itself a whole debate.Precisely, what Engels gets at there is that mathematicians are doing these operations without any understanding of where they came from. In fact in any college level calculus class, by the end of the 1st semester usually students have completely forgotten how to do even the limit definition of a derivative, let alone the way that that the derivative was developed, because there are all these little tricks and patterns that were discovered that would make this process much quicker to compute by hand (For example: The power rule, the quotient rule etc).
Well Archimedes is really the one who came up with the method of exhaustion, which was later developed into the infinite series, but the main contention to Leibniz and Newton and their infinitesimal from the mathematics community at the time was really that they could use the method of exhaustion and the infinite series to compute very close estimates and that these involved purely numbers, so why bother with this infinitesimal thing that doesn’t even really appear to be mathematics?
Honestly it’s very impressive that you have even begun asking the questions at such an early stage. This level of curiosity will absolutely serve you well. I would certainly caution you that the way mathematics is presented at first seems to give it the impression that it is really for calculating numbers that we need in engineering or science. But the reality is that, computers pretty much do all of that for us pretty well. So what actual use is it to learn mathematics? Well, I believe that I’ve made a pretty good case for using towards the dialectical development of knowledge in the total system of science with mathematics playing the role of developing conceptualizations to propel forward the sciences, and using the sciences to propel it forward as well, and that of course can come from an engineer just the same as a scientist. In fact in some sense, engineering is the born synthesis of a mathematician and a scientist, and the first step in orienting scientists and mathematicians towards where they should focus their efforts.
Oh thank you for the warm welcome. I’ve been a lurker for awhile and always loved the quality of discussions here, so finally decided to make an account. Also at the end of the day we’re both also comrades and are on equal ground, and in a real sense the process of discussion on this has helped me learn about this in deeper ways too, so sincerely thank you for posting this thread. I think it was Fanon who talks about how the teacher is a student and I just just hope that this very long response may be of use to you or anyone else.
Thanks again for your impressive response, sorry for not being able to add much to the beginning of your reply, but I agree completely and this has made me change the way I perceive mathematics, I will try to read these texts as soon as possible to see if I can get a better grasp of mathematics from a dialectical materialist point of view.
I really agree with this part, I don’t think most of our class really understand what a derivative is and how to get there, myself included, possibly. With the limit definition of a derivative you mean for example how you get from
X³to3X²? If that’s so, it’s one of the things they taught us the less, that didn’t even entered in the test, whenever we needed to derivative we just used the rules you mention.Isn’t this also a bit related to integrals? Since you are always working with abstract ideas in order to calculate the area of a surface. I haven’t worked with any integrals, though, just know what they are and they will teach it to me at the beginning of this year.
Thanks a lot for the good words, but I wish curiosity alone would produce better results, I drop out of high school and I was taught terribly at it so I’m struggling a lot, plus they basically told us “You already know x, y, z concepts” so I had to study some other stuff (which are basic, but I didn’t know them) on my own, and our physics teacher was the worst, she basically got mad at us because we didn’t understand physics… So yeah. Basically what you are saying is that mathematics serves to understand philosophy rather than numbers, lol. At least it works to understand the ideas behind how reality is structured, with which together with dialectical materialism can provide a huge tool to understand systems and concepts.
Well, good thing I created this post, then, lol. My Systema teacher (Russian martial arts) always tells me “Estudiante siempre, maestro a veces” (“Student always, teacher sometimes”) so I’m glad I also managed to give you something in return for your time invested.
deleted by creator