So I found out about Marx’ mathematical manuscripts, so I say “Hey, I’ve been studying mathematics this year at university. I understand limits and derivatives, maybe I can understand something of that gibberish.” So I see the titles and the one called “On the Concept of the Derived Function”, I go there and I see some notation I don’t understand, he speaks about things I’m not clearly understanding, so maybe some of you could make it clear.

For example:

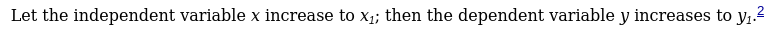
Why is this x sub 1 notation? Is this some other way to write derivatives? Because on the footnotes it says this:

  1. In order to avoid confusion with the designation of derivatives, Marx’s notation x´, y´, … for the new values of the variable has been replaced here and in all similar cases by x1, y1, …

Then I saw a talk about Marx’s mathematics and the infinitesimal and some of that stuff, but the one who was speaking didn’t went much into the mathematical part but was more like a history talk on how the Chinese were interested in the propositions of Marx because it liberated calculus from the idealist veil with which it was conceived by Leibniz and Newton, but the one who was talking mentioned Marx learning mathematics with whatever he had around and didn’t managed to read Cauchy so we was like “Yeah this is nice but it’s al shit now we have proved it fully works.” But well, he seems a bit biased, since he’s a Usonian, so maybe Marx’s writings are still relevant, I don’t even know who the fuck Cauchy is, so yeah, help.

Text: https://www.marxists.org/archive/marx/works/1881/mathematical-manuscripts/ch03.html

  • Soviet SnakeOPM
    4·
    2 years ago

    Thanks again for your impressive response, sorry for not being able to add much to the beginning of your reply, but I agree completely and this has made me change the way I perceive mathematics, I will try to read these texts as soon as possible to see if I can get a better grasp of mathematics from a dialectical materialist point of view.

    Precisely, what Engels gets at there is that mathematicians are doing these operations without any understanding of where they came from. In fact in any college level calculus class, by the end of the 1st semester usually students have completely forgotten how to do even the limit definition of a derivative, let alone the way that that the derivative was developed, because there are all these little tricks and patterns that were discovered that would make this process much quicker to compute by hand (For example: The power rule, the quotient rule etc).

    I really agree with this part, I don’t think most of our class really understand what a derivative is and how to get there, myself included, possibly. With the limit definition of a derivative you mean for example how you get from X³ to 3X²? If that’s so, it’s one of the things they taught us the less, that didn’t even entered in the test, whenever we needed to derivative we just used the rules you mention.

    Well Archimedes is really the one who came up with the method of exhaustion, which was later developed into the infinite series, but the main contention to Leibniz and Newton and their infinitesimal from the mathematics community at the time was really that they could use the method of exhaustion and the infinite series to compute very close estimates and that these involved purely numbers, so why bother with this infinitesimal thing that doesn’t even really appear to be mathematics?

    Isn’t this also a bit related to integrals? Since you are always working with abstract ideas in order to calculate the area of a surface. I haven’t worked with any integrals, though, just know what they are and they will teach it to me at the beginning of this year.

    Honestly it’s very impressive that you have even begun asking the questions at such an early stage. This level of curiosity will absolutely serve you well. I would certainly caution you that the way mathematics is presented at first seems to give it the impression that it is really for calculating numbers that we need in engineering or science. But the reality is that, computers pretty much do all of that for us pretty well. So what actual use is it to learn mathematics? Well, I believe that I’ve made a pretty good case for using towards the dialectical development of knowledge in the total system of science with mathematics playing the role of developing conceptualizations to propel forward the sciences, and using the sciences to propel it forward as well, and that of course can come from an engineer just the same as a scientist. In fact in some sense, engineering is the born synthesis of a mathematician and a scientist, and the first step in orienting scientists and mathematicians towards where they should focus their efforts.

    Thanks a lot for the good words, but I wish curiosity alone would produce better results, I drop out of high school and I was taught terribly at it so I’m struggling a lot, plus they basically told us “You already know x, y, z concepts” so I had to study some other stuff (which are basic, but I didn’t know them) on my own, and our physics teacher was the worst, she basically got mad at us because we didn’t understand physics… So yeah. Basically what you are saying is that mathematics serves to understand philosophy rather than numbers, lol. At least it works to understand the ideas behind how reality is structured, with which together with dialectical materialism can provide a huge tool to understand systems and concepts.

    Oh thank you for the warm welcome. I’ve been a lurker for awhile and always loved the quality of discussions here, so finally decided to make an account. Also at the end of the day we’re both also comrades and are on equal ground, and in a real sense the process of discussion on this has helped me learn about this in deeper ways too, so sincerely thank you for posting this thread. I think it was Fanon who talks about how the teacher is a student and I just just hope that this very long response may be of use to you or anyone else.

    Well, good thing I created this post, then, lol. My Systema teacher (Russian martial arts) always tells me “Estudiante siempre, maestro a veces” (“Student always, teacher sometimes”) so I’m glad I also managed to give you something in return for your time invested.