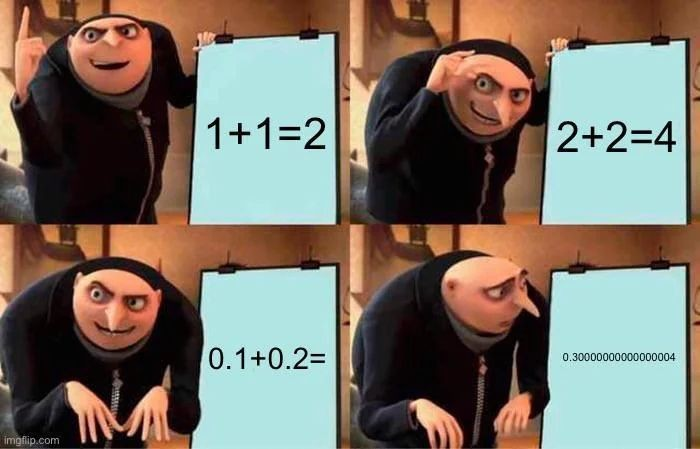Also 1-1 ≠ 0
Are you sure? I’ve never seen that inequality before.
Edit: and at least python agrees with me
print(0.1 + 0.2) # 0.300...0004 print(1.0-1.0) # 0.0I think it’s equal zero in this case. I’d have to look up the IEEE specification to make sure. AFAIK it’s just not guaranteed for any numbers and depends on the floating point implementation. A general rule of thumb for programmers is not to use ‘equal’ with floating point numbers.
The example is wrong, because they used
1.0.But in general
x-xdoes not have to equal0, that is true. I’m pretty sureNanandinfinitywould yield not0.0, butNaninstead.And if you reach x with two different calculations, e.g.
x1 = a - b - candx2 = a - c - bit is certainly not guaranteed thatx1 - x2 == 0.0This is correct. Additionally, if x is NaN, then x ≠ x.
It does.
x-x == 0is true unlessxis NaN or infinity.